IncomeLossCalculation

Calculation of probable income loss by deaths

The standard life tables come in the form of "the number of persons surviving to exact age x out of 100,000 births". This is the second column in the table below, the first column being age.

The third column is the probability of surviving 5 years, computed as the number of survivors at Age+5 / survivors at Age. For example at age 80 the probability of surviving 5 years is Survivors(85)/Survivors(80)=56373/72308=0.779623.

The estimated income in five years as a % of current is then the sum of (%income in each age band) multiplied by the probability of surviving five years in the middle of that age band. Givers without ages are omitted, assuming that they are similarly distributed.

Age band	% income	% 5 year survival	Product (% income)
<50	10%	99.99%	10%
51-60	16%	98%	16%
61-70	23%	96%	22%
71-80	30%	88%	26%
>80	21%	61%	13%
Total	99%		87%

So for example the 30% of current income coming from those in their 70s can be expected to decrease to 26% of current income.

The estimated income in 5 years is then 87% out of the 99% from givers for whom we have ages or estimated ages, or 85% of current income from those givers. Assuming that those without ages given are similarly distributed, we should expect a 15% reduction in 5 years from deaths.

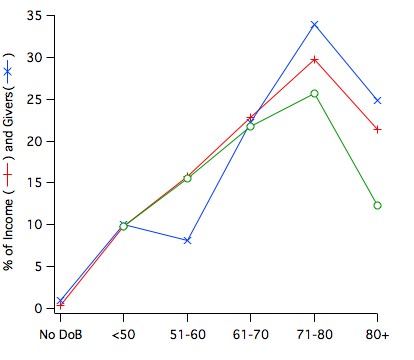
This is the giving profile. The blue curve is the distribution of planned givers, the red curve is the distribution of income, and the green curve is the most likely distribution of income in five years time.

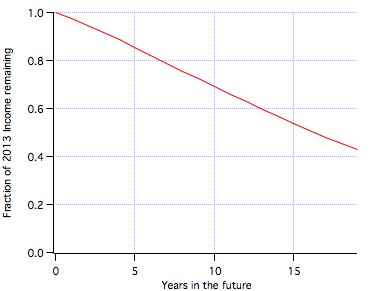
Repeating the procedure described above year by year for 20 years gives this curve

The data used follows:

Age	Survivors 1 year	Survival probability 5 years
0	100000	0.99482
1	99560	0.999106
2	99528	0.999327
3	99509	0.999437
4	99494	0.999508
5	99482	0.999558
6	99471	0.999598
7	99461	0.999628
8	99453	0.999628
9	99445	0.999608
10	99438	0.999547
11	99431	0.999437
12	99424	0.999286
13	99416	0.999105
14	99406	0.998924
15	99393	0.998783
16	99375	0.998682
17	99353	0.998621
18	99327	0.998601
19	99299	0.9986
20	99272	0.99857
21	99244	0.998549
22	99216	0.998508
23	99188	0.998468
24	99160	0.998397
25	99130	0.998336
26	99100	0.998264
27	99068	0.998173
28	99036	0.998071
29	99001	0.99796
30	98965	0.997838
31	98928	0.997675
32	98887	0.997522
33	98845	0.997329
34	98799	0.997125
35	98751	0.996881
36	98698	0.996616
37	98642	0.99632
38	98581	0.995983
39	98515	0.995615
40	98443	0.995205
41	98364	0.994775
42	98279	0.994292
43	98185	0.993777
44	98083	0.99323
45	97971	0.992651
46	97850	0.992018
47	97718	0.991353
48	97574	0.990643
49	97419	0.989889
50	97251	0.9891
51	97069	0.988266
52	96873	0.987334
53	96661	0.986282
54	96434	0.985057
55	96191	0.983647
56	95930	0.982029
57	95646	0.980219
58	95335	0.978266
59	94993	0.976177
60	94618	0.973937
61	94206	0.971552
62	93754	0.968983
63	93263	0.966128
64	92730	0.962914
65	92152	0.959263
66	91526	0.955051
67	90846	0.950212
68	90104	0.944653
69	89291	0.938303
70	88398	0.931073
71	87412	0.922917
72	86323	0.913731
73	85117	0.903415
74	83782	0.891767
75	82305	0.878537
76	80674	0.863488
77	78876	0.846303
78	76896	0.826714
79	74714	0.804521
80	72308	0.779623
81	69661	0.751884
82	66753	0.721361
83	63571	0.688128
84	60109	0.652382
85	56373	0.61439
86	52377	0.57468
87	48153	0.533923
88	43745	0.492925
89	39214	0.452491
90	34635	0.413426
91	30100	0.376312
92	25710	0.341579
93	21563	0.309512
94	17744	0.280207
95	14319	0.253789
96	11327	0.23007
97	8782	0.209064
98	6674	0.19059
99	4972	0.174377
100	3634	0.160429
101	2606	0.14812
102	1836	0.1378
103	1272	0.128931
104	867	0.121107

DavidMorgan Dec 2013